Have you ever wondered what a complete binary tree is and why it’s such an important idea in computer science? If you’re exploring data structures and algorithms, understanding complete binary trees is essential for your programming journey. Whether you’re just starting out or trying to strengthen your knowledge through a structured C programming course in Noida, this guide will cover everything you need to know about complete binary trees.
Understanding the Fundamentals: What Is a Complete Binary Tree?
When someone asks what a complete binary tree is, the answer lies in its unique structural properties. A complete binary tree is a specific type of binary tree where all levels are completely filled except possibly the last level. The last level is filled from left to right. Think of it like filling seats in a theater. You fill each row completely before moving to the next one. In the last row, you fill from left to right without leaving gaps.
This definition might sound simple, but the implications are significant. Complete binary trees have properties that make them very useful in various algorithms and data structures. They are the foundation of heap data structures, priority queues, and many sorting algorithms that you will encounter in any C programming course in Noida.
The importance of understanding a complete binary tree is in recognizing how this structure optimizes memory usage and provides consistent performance characteristics. Unlike general binary trees that can become unbalanced and inefficient, complete binary trees maintain a balanced structure. This ensures optimal performance for many operations.
Visual Understanding: How Complete Binary Trees Look
To truly grasp what is complete binary tree is, let’s visualize the concept. Imagine a pyramid where each level is completely filled before the next level begins. Here’s how a complete binary tree with 10 nodes would look:
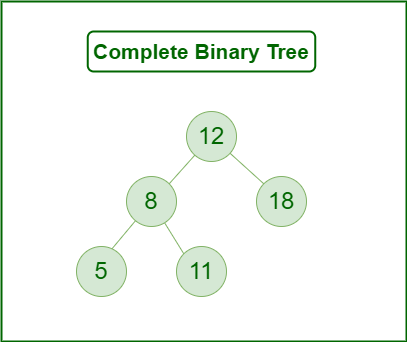
1
/ \
2 3
/ \ / \
4 5 6 7
/ \ /
8 9 10
Notice how levels 1, 2, and 3 are completely filled, while level 4 is filled from left to right. This is the defining characteristic that answers what is complete binary tree is in the most visual way possible.
Students learning data structures in a C programming course in Noida often find this visual approach helpful because it immediately clarifies the difference between complete binary trees and other tree structures. The left-to-right filling pattern is crucial and distinguishes complete binary trees from perfect binary trees (where all levels are completely filled) and full binary trees (where every node has either 0 or 2 children).
Properties That Make Complete Binary Trees Special
Understanding what a complete binary tree is requires knowing its key properties. These characteristics make complete binary trees very useful in programming:
Height Efficiency: A complete binary tree with n nodes has a height of ⌊log₂(n)⌋. This height makes it efficient for search and traversal operations. This logarithmic height is one of the main reasons why heap data structures, which are built as complete binary trees, work so well.
Array Representation: One of the most elegant features of complete binary trees is how easily they can be represented using arrays. For any node at index i, its left child is at index 2i+1, and its right child is at index 2i+2. The parent of any node, except the root, is at index ⌊(i-1)/2⌋. This property is widely discussed in educational programs, such as a C programming course in Noida.
Memory Optimization: Since complete binary trees can be stored in arrays without wasting space, they are very memory-efficient. There are no null pointers or wasted array indices, making them ideal for situations where memory use is important.
Predictable Structure: The left-to-right filling pattern ensures that the tree structure is always predictable. This predictability simplifies many algorithms that work on the tree.
Implementing Complete Binary Trees in C
Now that we understand what is complete binary tree is, let’s see how to implement one in C. This practical implementation will solidify your understanding and show you how these concepts translate into real code:
c#include <stdio.h>
#include <stdlib.h>
typedef struct {
int *data;
int size;
int capacity;
} CompleteBinaryTree;
// Initialize a complete binary tree
CompleteBinaryTree* createTree(int capacity) {
CompleteBinaryTree *tree = (CompleteBinaryTree*)malloc(sizeof(CompleteBinaryTree));
tree->data = (int*)malloc(capacity * sizeof(int));
tree->size = 0;
tree->capacity = capacity;
return tree;
}
// Insert a new element (maintains complete binary tree property)
int insert(CompleteBinaryTree *tree, int value) {
if (tree->size >= tree->capacity) {
printf(“Tree is full!\n”);
return 0;
}
tree->data[tree->size] = value;
tree->size++;
return 1;
}
// Get parent index
int getParent(int index) {
return (index – 1) / 2;
}
// Get left child index
int getLeftChild(int index) {
return 2 * index + 1;
}
// Get right child index
int getRightChild(int index) {
return 2 * index + 2;
}
// Display the tree level by level
void displayTree(CompleteBinaryTree *tree) {
if (tree->size == 0) {
printf(“Tree is empty!\n”);
return;
}
printf(“Complete Binary Tree: “);
for (int i = 0; i < tree->size; i++) {
printf(“%d “, tree->data[i]);
}
printf(“\n”);
}
This implementation demonstrates the core concepts that answer what is complete binary tree is in practical terms. Students in a C programming course in Noida would work through similar implementations to understand how theoretical concepts translate into working code.
Complete Binary Trees vs Other Tree Types
Understanding what a complete binary tree is becomes clearer when we compare it with other tree structures. This comparison is important for anyone who wants to master data structures.
Complete vs Perfect Binary Trees: Complete binary trees have all levels filled except possibly the last, which fills from left to right. Perfect binary trees have all levels fully filled. Every perfect binary tree is complete, but not every complete tree is perfect.
Complete vs Full Binary Trees: Full binary trees require every node to have either 0 or 2 children. However, they do not have the level-filling requirement of complete binary trees. A tree can be full without being complete, and vice versa.
Complete vs Balanced Binary Trees: Balanced trees maintain a height difference of at most 1 between left and right subtrees. In contrast, complete trees focus on filling levels. Complete binary trees are always balanced, but balanced trees aren’t necessarily complete.
These distinctions are fundamental concepts that any quality C programming course in Noida covers in depth, as they form the basis for understanding more complex data structures and algorithms.
Applications and Real-World Uses
Knowing what a complete binary tree is becomes even more valuable when you understand where these structures are used in real-world programming.
Heap Data Structures: Both min-heaps and max-heaps are built as complete binary trees. This structure ensures that heap operations like insertion, deletion, and finding the minimum or maximum element can be done efficiently in O(log n) time.
Priority Queues: Since priority queues are often built using heaps, they inherit the complete binary tree structure. This makes them highly efficient for tasks like scheduling, graph algorithms, and simulation systems.
Heap Sort Algorithm: Heap sort, one of the most elegant sorting algorithms, relies entirely on the properties of complete binary trees. Understanding what a complete binary tree is is essential for implementing and optimizing heap sort.
Binary Heap in Operating Systems: Many operating system schedulers use binary heaps, which are built as complete binary trees, to manage process priorities and resource allocation.
The Importance of Structured Learning
While you can learn what a complete binary tree is through self-study, structured learning environments offer clear benefits. A good C programming course in Noida provides:
Progressive Curriculum: Concepts build on each other logically. This ensures you grasp the basics before moving to more advanced topics.
Hands-On Practice: Regular coding exercises and projects reinforce what you learn in theory with practical use.
Expert Guidance: Experienced instructors can clarify complex ideas and offer insights from the industry.
Peer Learning: Working with fellow students improves understanding through discussion and problem-solving.
Industry Relevance: Course content matches current industry needs and programming practices.
Frequently Asked Questions (FAQs)
Q1. What is a complete binary tree in simple terms?
A complete binary tree is a tree where all levels are fully filled except the last, which fills from left to right.
Q2. How does a complete binary tree differ from a perfect binary tree?
A perfect binary tree has all levels filled, while a complete binary tree allows the last level to be partially filled from the left.
Q3. Why are complete binary trees important in C programming?
They form the foundation for heaps, priority queues, and efficient algorithms like heap sort.
Q4. How is a complete binary tree represented in an array?
Each node is stored level by level. Left child at 2i+1, right child at 2i+2, and parent at ⌊(i-1)/2⌋.
Q5. What are real-world uses of complete binary trees?
They are used in heaps, scheduling, priority queues, operating system resource allocation, and sorting algorithms.
Q: What is the main difference between complete and perfect binary trees?
A: A perfect binary tree has all levels completely filled, while a complete binary tree allows the last level to be partially filled (from left to right).
Q: Why are complete binary trees important in programming?
A: They provide optimal memory usage, predictable performance, and serve as the foundation for heaps, priority queues, and efficient sorting algorithms.
Q: How do you represent a complete binary tree in an array?
A: Store nodes level by level from left to right. For any node at index i: left child is at 2i+1, right child at 2i+2, parent at ⌊(i-1)/2⌋.
Q: What’s the height of a complete binary tree with n nodes?
A: The height is ⌊log₂(n)⌋, making operations very efficient even for large numbers of nodes.
Q: Can a complete binary tree be unbalanced?
A: No, complete binary trees are always balanced due to their level-by-level filling pattern.
Q: How does understanding complete binary trees help with other algorithms?
A: They’re fundamental to heap operations, sorting algorithms, priority queues, and many graph algorithms, making them essential for advanced programming concepts.




